Strahlenoptik bzw. Geometrische Optik
Die Strahlenoptik (auch als Geometrische Optik bezeichnet) befasst sich mit der Ausbreitung von Lichtstrahlen sowie mit der Interaktion von Lichtstrahlen mit Medien, die um ein Vielfaches größer sind als die Wellenlänge des Lichts.
In einem ersten Kapitel klären wir zunächst wie sich Lichtstrahlen ausbreiten und welche Geschwindigkeit Licht überhaupt hat. Dann behandeln wir im folgenden Kapitel den Effekt der Reflexion von Licht an spiegelnden Oberflächen und gehen insbesondere auf Hohlspiegel und Wölbspiegel ein. Im folgenden Kapitel behandeln wir schließlich den Effekt der Lichtbrechung und betrachten als Anwendungsbeispiele einen Lichtwellenleiter, eine Glasplatte und ein Glasprisma.
Diese Seite liefert eine einfache Beschreibung der Strahlenoptik mit Experimenten, die man leicht selbst nachmachen kann. Einige mathematische Gleichungen werden gezeigt ohne zu sehr auf die Details der Herleitung und Mathematik einzugehen. Auch werden wichtige Begriffe wie Reflexion, Brechung, Brennpunkt etc. erläutert - Begriffe, die für weitere Seiten rund ums Thema Optik Voraussetzung sind.
Einordnung der Strahlenoptik als Teilgebiet der Optik
Die Optik ist die Lehre vom Licht - Licht, das wir mit unseren Augen wahrnehmen. Die Optik ist ein großes Gebiet im Bereich der Physik, das sich in mehrere Teilgebiete untergliedern lässt, die historisch im Laufe der Jahrhunderte nach und nach entdeckt und erforscht wurden.
Im Jahre 1672 entwickelte Newton die sogenannte Korpuskeltheorie, nach der sich ein Lichtstrahl aus einzelnen Teilen (Korpuskeln) zusammensetzt. Solche Lichtstrahlen breiten sich geradelinig aus, werden an Flächen ganz oder teilweise reflektiert oder auch gebrochen, ehe sie vom menschlichen Auge wahrgenommen werden. Mit Newtons Korpuskulartheorie konnten jedoch nicht alle Effekte des Lichtes erklärt werden. Spezielle Effekte wie Beugung, Interferenz oder Polarisation konnten erst später mit der Wellentheorie des Lichtes nach Huygens (1678) und Young (1802) erklärt werden.
Im Jahre 1865 schließlich wurde Licht von Maxwell als elektromagnetische Welle beschrieben (siehe dazu auch unsere Seite über Farbmodelle). Demzufolge ist Licht eine elektromagnetische Welle, die sich mit Lichtgeschwindigkeit ausbreitet. Bis heute noch lassen sich gewisse Lichteffekte besser mit der Teilchenoptik und andere besser mit der Wellenoptik beschreiben; daher wird bei der Beschreibung von Licht auch der Begriff Welle-Teilchen-Dualismus verwendet. Erst seit der Entdeckung der Quantenoptik wurde ein theoretisches Beschreibungsmodell gefunden, das beide Aspekte in einer Theorie vereint.
Die Strahlenoptik bzw. Geometrische Optik (beide Begriffe werden synonym verwendet) ist ein Teilbereich der Optik, bei der die Wellenlänge des Lichtes sehr klein im Vergleich zu Objekten, mit denen das Licht in Wechselwirkung tritt, ist. Die obige Grafik zeigt, dass das sichtbare Licht einen Wellenlängenbereich zwischen 380 und 780 nm hat (die Wellenlänge ist also kleiner als ein Tausendstel Millimeter). Solche Lichtstrahlen treten mit Gegenständen wie Spiegeln, Glasflächen, Linsen, Blenden oder dem menschlichen Auge in Wechselwirkung; solche Objekte sind millionenfach größer.
Die Strahlenoptik beschreibt Effekte, die an solchen Gegenständen auftreten können: einfache Spiegelung (Reflexion), Ablenkung (Brechung) oder Aufspaltung eines Lichtstrahles (z.B. an einem Prisma). Spezielle Effekte wie Beugung und Interferenz spielen sich ab, wenn zwei Lichtstrahlen ähnlicher Wellenlänge aufeinandertreffen; diese Effekte können mit der Strahlenoptik nicht mehr beschrieben werden.
Lichtstrahlen und Lichtausbreitung
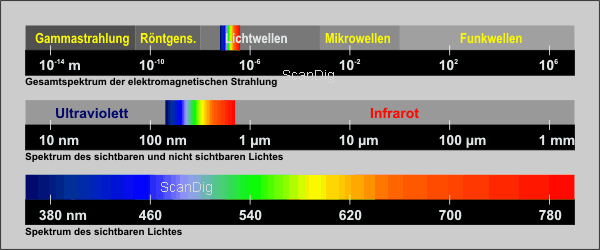
In diesem Kapitel möchte ich zunächst anhand von Bildern einige grundlegende Begriffe und Zusammenhänge aus dem Bereich der Optik erläutern, die in den folgenden Kapiteln immer wieder gebraucht werden. Lichtstrahlen breiten sich geradlinig aus; entspringen Lichtstrahlen von einer punktförmigen Lichtquelle L, so breiten sich die Strahlen homozentrisch, d.h. gleichmäßig in alle Richtungen, aus (siehe nebenstehende Abbildung). Man spricht deshalb auch von Kugelwellen.
Treffen homozentrische Lichtstrahlen auf eine Blende B, so entsteht hinter der Blende ein Lichtkegel, dessen Scheitelpunkt im Zentrum der Lichtquelle ist. Im Gegensatz dazu gibt es parallele Strahlenbündel, d.h. die Lichtstrahlen breiten sich nicht kegelförmig sondern parallel aus. Solche Parallelstrahlen erhält man zum Beispiel von einem Laserpointer oder auch von der Sonne. Die Sonne strahlt zwar kugelförmig in alle Richtungen Licht aus; da der Abstand zur Erde jedoch so groß im Vergleich zum Sonnendurchmesser ist, kann man bei den eintreffenden Sonnenstrahlen von Parallelstrahlen sprechen.
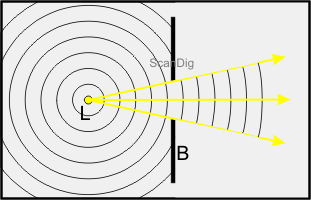
Licht breitet sich geradlinig aus. In nebenstehender Abbildung erkennt man Lichtstrahlen, die von der Lichtquelle L ausgesandt werden und auf einen Gegenstand G treffen. Hinter dem Gegenstand G bildet sich der sogenannte Kernschatten K. In diesen Bereich gelangt auf direktem Wege kein Lichtstrahl von der Lichtquelle L, so dass der entsprechende Bereich auf dem dahinter liegenden Schirm S theoretisch dunkel sein müsste. Ich sage deshalb theoretisch und habe auch den Kernschatten nicht schwarz sondern dunkelgrau gezeichnet, weil natürlich dennoch Licht durch Reflexion in den Bereich fällt. Sonst würde sich ja vor einem, wenn die Sonne von hinten scheint, ein rabenschwarzes Feld als Schatten auf der Straße bilden.
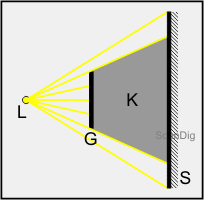
Betrachten wir nun das nächste Bild, auf dem zwei Lichtquellen L1 und L2 Licht auf den Gegenstand G strahlen. Von beiden Lichtquellen sind nur die jeweiligen zwei Grenzstrahlen eingezeichnet, die jeweils an der Oberkante und Unterkante des Gegenstandes G vorbeiziehen. Bei dieser Konstellation erhalten wir drei unterschiedliche Schattenbereiche hinter dem Gegenstand: Wie im vorigen Beispiel mit einer einzigen Lichtquelle erhalten wir wieder einen Kernschatten K; in diesen Bereich tritt weder Licht von der Lichtquelle L1 noch Licht von der Lichtquelle L2. Anders ausgedrückt: Steht eine Person im Feld K, so kann diese keine der beiden Lichtquellen direkt sehen. Außer dem Kernschattenbereich K gibt es noch zwei weitere Schattenbereiche H, die als Halbschatten bezeichnet werden. Diese Halbschatten-Bereiche zeichnen sich dadurch aus, dass sie jeweils nur von einer Lichtquelle angestrahlt werden, von der anderen aber nicht. Ein Beobachter, der im oberen Halbschattenbereich steht, wird voll von der Lichtquelle L1 angestrahlt, sieht aber die Lichtquelle L2 überhaupt nicht. Ich habe die beiden Halbschattenbereiche deshalb hellgrau gezeichnet, weil sie ja jeweils beleuchtet werden, aber eben nur von einer einzigen Lichtquelle, während die andere ihren Schatten in den Bereich wirft.
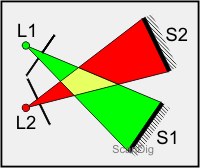
Eine wichtige Eigenschaft von Lichtstrahlen möchte ich an dieser Stelle noch erwähnen: Lichtstrahlen können sich durchkreuzen; sie beeinflussen sich dabei gegenseitig nicht. In der nebenstehenden Abbildung sind zwei Lichtquellen L1 und L2 eingetragen, die jeweils durch eine Blende hindurch Licht auf die Schirme S1 und S2 strahlen. Die Lichtquelle L1 strahlt grünes Licht ab, während die Lichtquelle L2 rotes Licht aussendet. Auf den beiden Schirmen kommt jeweils nur das rote bzw. grüne Licht an. Beim Kreuzen zweier Lichtstrahlen verhalten sich diese also jeweils so als wäre der andere gar nicht vorhanden. Nur in demjenigen Bereich, wo sich die beiden Lichtstrahlen treffen, können sich durch Farbaddition neue Farben bilden; aus rot und grün wird zum Beispiel gelb, siehe dazu unsere Seite über Farbmodelle.
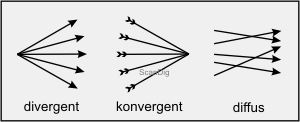
Bei der Beschreibung von Lichtstrahlen werden immer wieder die Begriffe konvergent, divergent und diffus verwendet. Die nebenstehende Grafik veranschaulicht diese drei Ausbreitungsarten von Licht. Divergente Lichtstrahlen entstammen einem gemeinsamen Punkt und breiten sich radial in alle Richtungen aus, zum Beispiel von einer punktförmigen Lichtquelle aus. Konvergente Strahlen kommen aus verschiedenen Richtungen und laufen auf einen gemeinsamen Schnittpunkt zu, zum Beispiel wenn die Lichtstrahlen über einen Parabolspiegel gebündelt werden. Lichtstrahlen, die weder einen gemeinsamen Ursprungsort noch einen gemeinsamen Zielort haben, bezeichnet man als diffus.
Lichtgeschwindigkeit
Bleibt zum Abschluss dieses Kapitels noch die Frage zu klären, mit welcher Geschwindigkeit sich ein Lichtstrahl ausbreitet. Es ist dies natürlich die Lichtgeschwindigkeit. Aber wie groß ist die Lichtgeschwindigkeit? Ist sie überall gleich, egal ob in der Luft oder im Wasser?
| Medium |
Lichtgeschwindigkeit |
| Vakuum |
300.000 km/s |
| Luft |
300.000 km/s |
| Wasser |
224.000 km/s |
| Quarz |
194.000 km/s |
| Glas |
190.000 km/s |
| Diamant |
122.000 km/s |
Zunächst sei einmal erwähnt, dass die Lichtgeschwindigkeit eine universelle Konstante ist und demnach auch unabhängig von der Wellenlänge des Lichtes ist. Allerdings bewegt sich das Licht nicht überall mit gleicher Geschwindigkeit fort. Die Lichtgeschwindigkeit hat im Vakuum ihren höchsten Wert von ca. 300.000 km/s. In Luft ist der Zahlenwert nur unwesentlich kleiner. In Wasser hingegen breitet sich Licht ca. 25% langsamer fort als in Luft; in Glas hat die Lichtgeschwindigkeit nicht einmal mehr zwei Drittel ihres Wertes im Vakuums. Die obige Tabelle zeigt ungefähre Zahlenwerte für die Lichtgeschwindigkeit in unterschiedlichen lichtdurchlässigen Medien.
Lichtgeschwindigkeit im Vakuum: c0 = 299.792.458 m/s
Um sich von der Größe der Lichtgeschwindigkeit ein Bild zu machen seien ein paar Beispiele erwähnt: Die Erde hat am Äquator einen Umfang von ca. 42.000 km. Während ein normales Passagierflugzeug ungefähr 2 Tage für eine Komplettumrundung bräuchte schafft es ein Lichtstrahl in etwas mehr als einer Zehntel Sekunde. Die Entfernung des Mondes von der Erde beträgt ungefähr 400.000 km. Licht, das vom Mond auf die Erde kommt, ist also etwas mehr als eine Sekunde unterwegs. Unsere Sonne, die uns täglich Licht spendet, ist im Mittel ca. 150 Millionen Kilometer von der Erde entfernt. Für diese Entfernung benötigt das Licht immerhin 500 Sekunden, d.h. bei einem Blick in die Sonne sehen wir diese, wie sie vor ca. 8 Minuten ausgesehen hat, wir werfen also quasi einen Blick in die Vergangenheit.
Auch wenn man sich eine Strecke von 150 Millionen Kilometer kaum vorstellen kann ist dies immer noch eine Kurzstrecke in astronomischen Entfernungsangaben. In der Astronomie werden Entfernungen nicht mehr in Kilometern sondern in Lichtjahren angegeben. Dabei ist ein Lichtjahr diejenige Strecke, die ein Lichtstrahl zurücklegt, wenn er ein ganzes Jahr unterwegs ist. Dies entspricht einer Strecke von 9,5 Billionen Kilometern.
In der Astronomie werden Entfernungen nicht in Kilometern sondern in Lichtjahren angegeben. Ein Lichtjahr ist die Strecke, die Licht innerhalb eines Jahres mit Lichtgeschwindigkeit zurücklegt. Ein Lichtjahr entspricht einer Strecke von 9,5 · 1012 km.
Während das Licht von unserer Sonne zur Erde also ungefähr 8 Minuten unterwegs ist, braucht Licht vom nächst gelegenen Stern Alpha Centauri bereits 4,3 Lichtjahre, bis es auf die Erde gelangt. Betrachtet man also den Stern Alpha Centauri mit einem Teleskop so sieht man diesen wie er vor über 4 Jahren ausgesehen hat. Selbst eine Entfernungsangabe wie 4,3 Lichtjahre sind in der Astronomie noch kleine Dimensionen. Alleine der Durchmesser unserer Milchstraße beträgt ca. 100.000 Lichtjahre, andere Galaxien sind Millionen oder gar Milliarden von Lichtjahren entfernt.
Reflexion von Lichtstrahlen
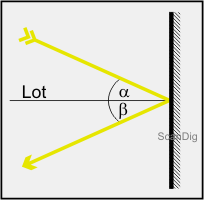
Nachdem wir nun grundlegende Kenntnisse über die Lichtausbreitung gewonnen haben, kommen wir zum ersten Effekt beim Zusammenspiel von Lichtstrahlen mit Gegenständen, nämlich der Reflexion an einer Oberfläche. In der nebenstehenden Abbildung ist ein Lichtstrahl eingezeichnet, der schräg mit einem Winkel α auf eine reflektierende Oberfläche trifft. Eine reflektierende Oberfläche ist zum Beispiel ein Glasspiegel, wie wir ihn alle kennen. Aber auch an Metallplatten oder Glasscheiben kann Reflexion von Licht auftreten. Der Winkel α wird als Einfallswinkel bezeichnet. Er wird relativ zur Senkrechten der Oberfläche gemessen; diese Senkrechte wird auch als Einfallslot, oder nur Lot, bezeichnet. Der einfallende Strahl wird an der spiegelnden Oberfläche reflektiert und tritt mit dem sogenannten Ausfallswinkel β wieder aus. Auch der Ausfallswinkel wird relativ zum Lot gemessen. Der einfallende Strahl, der reflektierte Strahl und das Lot liegen in einer Ebene. Bei der Reflexion von Lichtstrahlen an einer reflektierenden Oberfläche gilt das Reflexionsgesetz:
Reflexionsgesetz: Einfallswinkel = Ausfallswinkel bzw. α = β
Das Reflexionsgesetz gilt grundsätzlich bei der Reflexion von Lichtstrahlen, auch wenn die reflektierende Oberfläche nicht eben ist oder diffuses Licht einfällt. Dann gilt für jeden einzelnen Lichtstrahl am jeweiligen Auftreffpunkt auf der Oberfläche individuell das Reflexionsgesetz.
Reflexion an einem ebenen Spiegel
Betrachten wir nun als Beispiel für die Reflexion von Lichtstrahlen einen ebenen Spiegel, so wie wir ihn alle vom Badezimmer her kennen. Im Bild ist dieser Spiegel mit S bezeichnet. Von einem Gegenstand G aus treffen Lichtstrahlen auf diesen Spiegel und werden gemäß dem Reflexionsgesetz so reflektiert, dass der Ausfallswinkel gleich dem Einfallswinkel ist. Die reflektierten Lichtstrahlen fallen dann auf das Auge A des Betrachters, der in den Spiegel schaut. Im Bild sind diejenigen beiden Strahlen eingezeichnet, die das Auge gerade noch wahrnehmen kann.
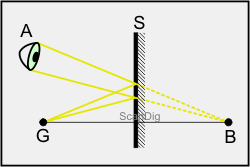
Natürlich befindet sich innerhalb der beiden Strahlen ein ganzes Strahlenbündel, das auf das Auge trifft. Und natürlich treffen auch noch andere Lichtstrahlen vom Punkt G auf den Spiegel; diese werden jedoch unter anderen Winkeln reflektiert, so dass sie von diesem eingezeichneten Auge nicht mehr eingefangen werden können, wohl aber vielleicht von einer daneben stehenden Person. Betrachten wir nun die Verlängerungen der reflektierten Strahlen, dann erkennen wir, dass diese sich hinter dem Spiegel im Punkt B schneiden. Für das Auge A scheinen die Strahlen also vom Punkt B herzukommen, weshalb dieser Punkt B auch als Bildpunkt bezeichnet wird.
Anhand des Bildes erkennen wir sofort, dass der Gegenstandspunkt G und der Bildpunkt B auf einer Normalen zur Spiegelfläche liegen; sie haben beide den gleichen Abstand zum Spiegel. Das Auge sieht also nicht den eigentlichen Gegenstand G sondern nur das virtuelle Bild B. Ein normaler Spiegel erzeugt also keine echten Bilder sondern nur scheinbare (virtuelle) Bilder, die symmetrisch mit dem eigentlichen Gegenstand zum Spiegel liegen. Man spricht deshalb auch vom Spiegelbild des Gegenstandes.
Reflexion am Hohlspiegel (Konkavspiegel)
Wie wir weiter oben gelernt haben, gilt das Reflexionsgesetz auch an nicht ebenen Flächen, zum Beispiel an einem Hohlspiegel. Ein sphärischer Hohlspiegel, wie er im Bild dargestellt ist, ist eine innen verspiegelte Kugelkalotte. Trifft ein Lichtstrahl in den Hohlspiegel, so wird er gemäß dem Reflexionsgesetz am Einfallslot gespiegelt. Dabei ist das Einfallslot die Senkrechte auf die Tangentialebene am Auftreffpunkt des Lichtstrahls. Trifft ein achsenparalleler Strahl ins Innere des Hohlspiegels wird er so reflektiert, dass er durch den Brennpunkt F geht. Solche achsenparallele Strahlen werden auch als Paraxialstrahlen bezeichnet.
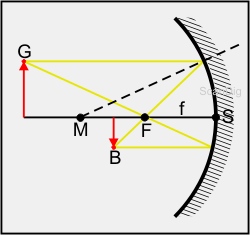
Der Brennpunkt befindet sich auf der optischen Achse, und zwar in der Mitte zwischen dem Kugelmittelpunkt M und dem Scheitelpunkt S. Die dazugehörige Brennweite f halbiert also den Radius der Kugel, die den Hohlspiegel bildet. Schickt man ein Bündel von achsenparallelen Strahlen in einen Hohlspiegel hinein, so versammeln sich sämtliche Strahlen im Brennpunkt. In diesem Punkt befindet sich also der hellste Fleck, und an dieser Stelle wird es unter Umständen sehr heiß. Wichtig zu bemerken ist, dass sich nur achsennahe Strahlen im Brennpunkt treffen. Sollen sich auch weiter von der optischen Achse entfernte Lichtstrahlen im Brennpunkt vereinigen, so muss anstelle eines Hohlspiegels ein Parabolspiegel verwendet werden. Eine Anwendung von Parabolspiegeln sind Auto-Scheinwerfer oder natürlich Parabolantennen. Parabolantennen sammeln parallel einfallende Strahlen im Brennpunkt, wo sich ein Detektor befinden muss; dadurch werden viele einfallende Strahlen gesammelt, und somit erfolgt eine Signalverstärkung. Bei Parabolscheinwerfern befindet sich im Brennpunkt ein Lämpchen, das in Richtung des Spiegels strahlt. Die vom Brennpunkt in alle Richtungen ausgestrahlten Lichtstrahlen werden vom Spiegel als Parallelstrahlen ausgesendet. Dadurch erhält man ein gut gebündeltes Scheinwerferlicht.
Wie entsteht nun das Bild beim Hohlspiegel? Betrachten wir dazu obige Abbildung, wo ein Gegenstand G auf sein Bild B abgebildet wird. Man erhält den Bildpunkt B als Schnittpunkt von zwei Strahlen: Der achsenparallele Strahl, der von G in Richtung Spiegel ausgesendet wird, wird so reflektiert, dass er durch den Brennpunkt verläuft. Ein zweiter Lichtstrahl, der von G aus durch den Brennpunkt in Richtung Spiegel strahlt, wird am Spiegel so reflektiert, dass er parallel wieder austritt. Als Schnittpunkt der beiden Linien erhält man den Bildpunkt B. Es handelt sich um ein reelles Bild, das aber auf dem Kopf steht; man spricht daher von einem umgekehrten Bild. Aufrechte Bilder erhält man am Hohlspiegel nur, wenn man den Gegenstand zwischen Spiegel und Brennpunkt F stellt; das Spiegelbild wird dann zwar aufrecht aber virtuell, da sich die reflektierten Strahlen dann hinter dem Spiegel schneiden.
Wie kann man nun ein Spiegelbild im Hohlspiegel betrachten? Anhand der Abbildung wird klar, dass sich die Lichtstrahlen des Gegenstandes G im Bildpunkt B wieder treffen. Der Bildpunkt B ist demnach der einzige Punkt, der ein scharfes Abbild des ursprünglichen Gegenstandes liefert. Hier muss sich das Auge des Betrachters befinden, um den Gegenstand G scharf erkennen zu können. Befindet sich das Auge im äußerst nahen Umkreis von B, so ist das Bild zwar noch erkennbar, ist aber unscharf. Im weitern Umkreis von B sind nur noch grobe Züge des Gegenstandes zu erkennen, eventuell gerade noch einige Farbtöne, aber keine Details mehr. Der Betrachter muss also genau im Punkt B stehen; hier könnte auch ein Schirm, ein Film oder ein CCD-Chip liegen.
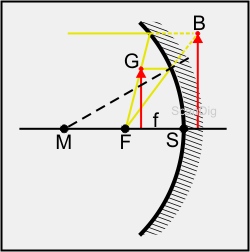
Betrachten wir nun den Fall, dass sich der Gegenstand ganz nahe am Spiegel befindet, im nebenstehenden Bild. Im Gegensatz zum obigen Bild haben wir den Gegenstand so nahe an den Hohlspiegel herangebracht, so dass die Gegenstandsweite kleiner als die Brennweite ist; der Gegenstand liegt also näher am Spiegel als dessen eigentlicher Brennpunkt. Bei der Konstruktion des Spiegelbildes verwenden wir wieder zwei Hauptstrahlen, nämlich den Brennpunktstrahl und den Paraxialstrahl. Der Brennpunktstrahl wird am Spiegel in einen achsenparallelen Strahl reflektiert; der achsenparallele Strahl verläuft nach der Reflexion durch den Brennpunkt. Die beiden reflektierten Strahlen schneiden sich aber hinter dem Spiegel; die entsprechenden Schnittlinien sind gestrichelt eingezeichnet. Im Schnittpunkt erhalten wir den Bildpunkt B. Wir erkennen sofort, dass unser Bild B des Gegenstandes G aufrecht ist; auch erkennen wir, dass das Bild größer als der ursprüngliche Gegenstand ist; allerdings handelt es sich um ein virtuelles Bild, das sich hinter dem Spiegel befindet.
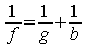
Die horizontale Entfernung zwischen dem Gegenstand und dem Scheitel S wird als Gegenstandsweite g bezeichnet; entsprechend wird die Bildweite mit b bezeichnet. Zusammen mit der Brennweite f zwischen dem Brennpunkt F und dem Scheitel S erhält man die Abbildungsgleichung des Hohlspiegels: Der Kehrwert der Brennweite f ist gleich der Summe der Kehrwerte aus Gegenstandsweite g und Bildweite b. Da die Brennweite an einem Hohlspiegel bekannt ist (halber Krümmungsradius) und man die Gegenstandweite einfach nachmessen kann, lässt sich mit der Abbildungsgleichung die Entfernung und damit auch die Größe des entstehenden Bildes berechnen. Zum Abschluss sei noch einmal erwähnt, dass diese Gleichung nur für achsennahe Strahlen gilt.
Ich möchte dieses bislang theoretische Kapitel mit einem praktischen Beispiel schließen. Anhand der obigen beiden Skizzen haben wir gelernt, dass ein Hohlspiegel reelle, umgekehrte und verkleinerte Bilder liefert, wenn sich der Gegenstand außerhalb der Brennweite befindet, dass er virtuelle, aufrechte und vergrößerte Bilder liefert, wenn der Gegenstand innerhalb der Brennweite liegt.


Diese beiden auf theoretischem Wege gewonnenen Erkenntnisse untersuchen wir nun mit einem ganz einfachen Kosmetikspiegel, den ich aus meinem Badezimmer entnehme. Ich positioniere den Hohlspiegel irgendwo fest im Raum und blicke von großer Entfernung in den Spiegel. Das linke Foto, das ich aus 3 Metern Entfernung mit einem Zoom-Objektiv gemacht habe, zeigt ein scharfes Bild, das der Hohlspiegel liefert: Ein Gartentisch steht auf dem Kopf und ist so verkleinert, dass er fast als Ganzes ins Bild passt. Bei der Aufnahme des Bildes musste ich an genau einen Punkt gehen, nämlich den Bildpunkt, um ein scharfes Spiegelbild zu sehen. Genau dies haben wir oben gelernt: Nur im Bildpunkt kann ein Betrachter stehen, um ein scharfes Bild zu sehen. Das rechte Foto habe ich schließlich aus 15 cm Entfernung gemacht, also ganz nah am Spiegel, weit innerhalb seiner Brennweite. Wir erkennen ein aufrechtes Bild, das meine Kamera vergrößert anzeigt. Genauso nutzen wir auch einen Kosmetikspiegel: Wir gehen ganz nah an den Spiegel heran, um in einer winzigen Augenwimper eine riesige Borste fein zu erkennen. Für größere Entfernungen ist ein Kosmetikspiegel nicht nutzbar.
Reflexion am Wölbspiegel (Konvexspiegel)
Nachdem wir nun gerade die Spiegelung am Hohlspiegel behandelt haben, kommen wir zum umgekehrten Fall, nämlich einem Wölbspiegel, auch Konvexspiegel genannt. Es handelt sich wieder um einen kugelförmigen Spiegel mit dem Kugelradius r, der jedoch nicht innerhalb der Kugelkalotte sondern außerhalb verspiegelt ist; man blickt also von außen auf die Kugeloberfläche drauf. Auch beim Wölbspiegel gilt das Reflexionsgesetz, so dass einfallende Lichtstrahlen am senkrecht zur Kugeloberfläche stehenden Einfallslot gespiegelt werden. Das folgende Bild zeigt einen Gegenstand G, der vor einem Wölbspiegel steht und dort gespiegelt wird.
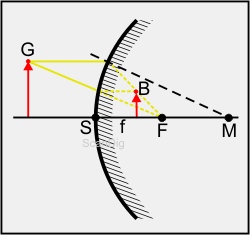
Wie entsteht das Bild an so einem Spiegel? Betrachten wir dazu wieder zwei Hauptstrahlen. Der achsenparallele Strahl, der von G aus auf die Kugeloberfläche trifft, geht definitionsgemäß durch den Brennpunkt F. Bei einem Wölbspiegel liegt der Brennpunkt jedoch nicht vor dem Spiegel, sondern er liegt dahinter, also innerhalb der Kugel. Daher habe ich den Lichtstrahl, der vom Gegenstand G aus in Richtung Kugeloberfläche verläuft, durchgehend gezogen, und den Lichtstrahl, der von der Kugeloberfläche zum Brennpunkt verläuft, gestrichelt. Es handelt sich um einen virtuellen Lichtstrahl, der nicht wahrlich existiert. Der zweite Hauptstrahl verläuft vom Gegenstand G direkt zum Brennpunkt F. Auch diesen habe ich vor der Kugel durchgehend und innerhalb der Kugel gestrichelt gezeichnet. Ein Brennpunktstrahl wird achsenparallel reflektiert; auch diese Reflektion findet innerhalb der Kugel statt, daher ist die achsenparallele Reflexionslinie gestrichelt gezeichnet. Aus dem Schnittpunkt der beiden reflektierten Hauptstrahlen erhält man den Bildpunkt B. Würden wir als dritten Lichtstrahl noch den Mittelpunktstrahl einzeichnen, so verliefe der vom Gegenstandspunkt G senkrecht durch die Kugeloberfläche hindurch zum Kugelmittelpunkt M. Natürlich würde auch der Mittelpunktstrahl die anderen Lichtstrahlen im Bildpunkt B schneiden.
Anhand des Bildes erkennt man sofort, dass das Bild B zwar kleiner als der Gegenstand G jedoch aufrecht ist. Allerdings handelt es sich um ein virtuelles Bild, das im innern der Kugel zu entstehen scheint. Wie kann man nun so ein virtuelles Bild betrachten? Gar nicht, ist die einfache und klare Antwort. Es handelt sich um kein reelles Bild, das mit einem Schirm oder einem CCD-Chip aufgefangen werden kann. Das Bild ist virtuell und befindet sich scheinbar hinter der spiegelnden Oberfläche, wo aber kein Betrachter stehen kann. Während ein Hohlspiegel also Lichtstrahlen eines Gegenstandes sammelt und in einem reellen Bildpunkt wiedergibt, zerstreut sie ein Konvexspiegel. Die reflektierten Lichtstrahlen scheinen zwar vom virtuellen Bild B herzukommen, aber ein außen stehender Betrachter kann in keinem Punkt ein brauchbares Bild erkennen. Fassen wir zum Abschluss des Kapitels die gewonnenen Erkenntnisse zusammen:
Am Hohlspiegel entsteht ein reelles, umgekehrtes Bild, das von einem Betrachter im Bildpunkt B aufgefangen werden kann. Am Wölbspiegel entsteht ein virtuelles, aufrechtes Bild, das von keinem Schirm aufgefangen werden kann. Der Hohlspiegel sammelt die Lichtstrahlen eines Gegenstandes G, der Wölbspiegel zerstreut die Lichtstrahlen.
Brechung von Lichtstrahlen
Im vorigen Kapitel haben wir den Effekt der Reflexion von Lichtstrahlen an spiegelnden Oberflächen behandelt. Jetzt kommen wir zum zweiten Effekt, der Brechung von Lichtstrahlen an lichtdurchlässigen Oberflächen. Während wir die Reflexion von Licht alltäglich am Badezimmerspiegel nutzen, treten uns Brechungseffekte von Licht nicht tagtäglich in Erscheinung.

Deshalb möchte ich dieses Kapitel mit einem kleinen Experiment beginnen, das jeder leicht nachvollziehen kann: Wir füllen eine Schale mit Wasser und tauchen ein Stäbchen oder einen Bleistift schräg ins Wasser ein (siehe nebenstehendes Bild). Betrachten wir nun das eingetauchte Stäbchen von vorne, dann hat es den Anschein, als wäre es an der Wasseroberfläche abgeknickt. Man glaubt sogar, dass es sich gar nicht um ein gerades Stäbchen handelt, sondern um ein Winkelstück. Tatsächlich aber beobachten wir hier den Effekt der Brechung von Licht: Licht, das von einem Medium (hier Wasser) ins andere (hier Luft) übergeht, wird an der Grenzfläche gebrochen. In das Bild habe ich noch eine schwarze Linie eingezeichnet, die die tatsächliche Position des Stäbchens wiedergibt; dadurch erkennt man deutlich den Knick, den das Stäbchen scheinbar an der Wasseroberfläche macht. Der Stein im Wasser dient übrigens nur zur Fixierung des Stabes, da dieser sonst von alleine wieder auftauchen würde. Behandeln wir nun im Folgenden den Effekt der Brechung etwas genauer.
Das Brechungsgesetz
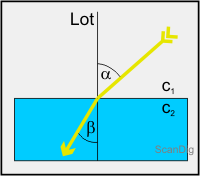
Im vorigen Teilkapitel haben wir anhand eines einfachen Experimentes festgestellt, dass das Licht eines Stabes, der in Wasser getaucht wird, an der Wasseroberfläche gebrochen wird. Diesen Sachverhalt beschreiben wir mathematisch mit dem Brechungsgesetz. Die nebenstehende Abbildung zeigt den Sachverhalt noch einmal anschaulich: Ein Lichtstrahl taucht vom Medium Luft in das Medium Wasser ein; der Eintrittswinkel ist α, gemessen zum Einfallslot hin. In der Luft bewegt sich das Licht noch mit der Lichtgeschwindigkeit der Luft c1; in Wasser ist die Lichtgeschwindigkeit c2 deutlich geringer, wie wir der obigen Tabelle der Lichtgeschwindigkeiten entnehmen können. Beim Eintritt vom Medium Luft in das Medium Wasser wird der Lichtstrahl zum Lot hingebrochen; der zugehörige Winkel ist mit β in der Skizze eingezeichnet.
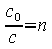
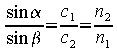
Das Snelliussche Brechungsgesetz beschreibt den Zusammenhang zwischen den Lichtgeschwindigkeiten und den Winkeln: Das Verhältnis der Lichtgeschwindigkeiten ist gleich dem Verhältnis der Sinusse der Winkel, und ebenso gleich dem umgekehrten Verhältnis der Brechzahlen. Weiter unten findet sich eine Tabelle mit einigen Brechzahlen für unterschiedliche Medien. Wir erkennen sofort, dass die Brechzahl von Luft nahezu identisch ist mit der Brechzahl für das Vakuum (ähnlich ist die Lichtgeschwindigkeit in der Luft nahezu identisch mit der Lichtgeschwindigkeit im Vakuum).
Setzen wir also für die Lichtgeschwindigkeit c1 der Luft die Vakuums-Lichtgeschwindigkeit c0 und für die Brechungszahl der Luft n2=1, dann erhalten wir eine einfache Definition der Brechungszahl für ein Medium gemäß nebenstehender Gleichung: Die Brechzahl ergibt sich als Quotient aus der Vakuums-Lichtgeschwindigkeit und der Lichtgeschwindigkeit im Medium. Die Brechzahl n wird auch als Brechungsindex bezeichnet.
| Medium |
Brechzahl n |
| Vakuum |
1,0000 |
| Luft |
1,0003 |
| Kohlendioxid |
1,0045 |
| Wasser |
1,333 |
| Glas |
1,5 - 1,9 |
| Diamant |
2,417 |
In der nebenstehenden Tabelle sind die Brechzahlen für eine Reihe von unterschiedlichen Medien aufgelistet. Wir erkennen sofort, dass die Brechzahlen in Gasen (Luft und CO2) nahezu identisch mit der Brechzahl 1 im Vakuum sind. Wasser hat eine Brechzahl von 1,333; in Festkörpern nimmt die Brechzahl sehr hohe Werte ein. Nehmen wir als Beispiel einen Lichtstrahl, der aus der Luft mit einem Winkel α = 45° in Wasser eintritt. Dann berechnet sich der Austrittswinkel β gemäß obiger Gleichung zu: β = arcsin[sin α / nWasser] = arcsin[sin 45° / 1,333] = 32°. Der einfallende Lichtstrahl wird also um 13° zum Lot hingebrochen. Das Medium mit der größeren Brechzahl bzw. mit der kleineren Lichtgeschwindigkeit wird übrigens auch als das optisch dichtere Medium bezeichnet. Allgemein wird vom optisch dichteren und optisch dünneren Medium gesprochen.
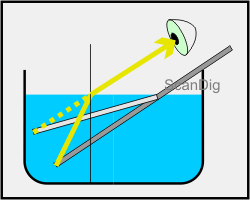
Ich möchte zum Abschluss dieses Teilkapitels noch einmal unser Experiment von oben betrachten. In der nebenstehenden Skizze ist der eingetauchte, reelle Stab dunkelgrau dargestellt. Infolge der Brechung sehen wir jedoch an der Wasseroberfläche einen Knick, und unter Wasser sehen wir den hellgrau dargestellten Stab. Den Effekt der Brechung erklären wir nun anhand des untersten Stabendes. Ein Lichtstrahl dringt vom untersten Stabende zur Wasseroberfläche (durchgezogene gelbe Linie) und wird beim Übergang in das optisch dünnere Medium (nämlich die Luft) vom Lot weggebrochen (durchgezogene gelbe Linie mit Pfeil). Dieses Licht gelangt dann ins Auge des Betrachters. Das Auge weiß jedoch nichts von der Brechung des Lichts und denkt sich, das Licht kommt vom hellgrauen Stab her (gepunktete gelbe Linie). Genau diesen Effekt haben wir mit dem obigen Foto beobachtet; der originale Stab unter Wasser ist mit einer schwarzen Linie eingezeichnet; das gebrochene Licht des Stabes ist auf dem Foto zu erkennen.
Grenzwinkel und Totalreflexion
Bei der Behandlung der Brechung und des Brechungsgesetz haben wir bislang immer den Fall betrachtet, dass der Lichtstrahl vom optisch dünneren Medium (Luft) in das optisch dichtere (Wasser) übergeht. Das Licht wird dabei zum Einfallslot hingebrochen. Wir haben bei unserem Beispiel mit dem Stab im Wasser auch schon den umgekehrten Fall kurz angesprochen, nämlich dass beim Übergang von Wasser zu Luft das Licht vom Lot weggebrochen wird. Diese normale Situation ist im linken der drei folgenden Bilder nochmals dargestellt: Der Lichtstrahl, der mit dem Winkel α im Wasser auf die Wasseroberfläche trifft, wird vom Lot weggebrochen, so dass der Ausfallswinkel β größer als der Einfallswinkel α ist.
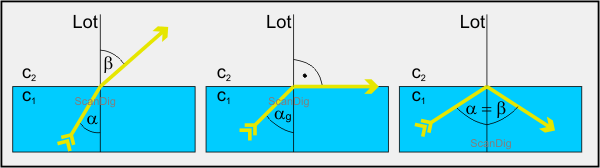
Man kann sich nun leicht vorstellen, dass bei allmählicher Vergrößerung des Winkels α irgendwann der Fall auftritt, wo der Austrittswinkel β genau 90° ist. Dann tritt der Lichtstrahl nicht mehr wirklich aus dem Wasser aus sondern verläuft senkrecht zum Lot auf der Wasseroberfläche. Dieser Grenzfall ist im mittleren Bild dargestellt. Da dies ein wirklicher Grenzfall ist, wird der zugehörige Winkel αg auch als Grenzwinkel oder Grenzwert bezeichnet.
Erhöht man schließlich den Einfallswinkel α noch mehr, so findet überhaupt keine Brechung des Lichtes mehr statt, sondern der Lichtstrahl wird total reflektiert. Der Ausfallswinkel β hat dann den gleichen Wert wie der Einfallswinkel α (siehe Reflexionsgesetz). Dieser Sachverhalt ist im ganz rechten der drei Bilder dargestellt. Es tritt also kein Licht mehr aus dem Wasser aus, sondern die gesamte Lichtmenge wird ins Wasser zurück reflektiert. Dieser Fall wird auch als Totalreflexion bezeichnet.
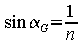
Behandeln wir nun den Brechungsindex mathematisch und verwenden dazu obige Gleichung 2. Im Grenzfall hat der Winkel β den Wert 90°, so dass der zugehörige Sinuswert 1 wird. Ist das Austrittsmedium Luft oder Vakuum, so ist n2=1, so dass sich Gleichung 2 zu nebenstehender Gleichung 4 vereinfacht. Demnach ist der Sinus des Grenzwinkels gleich dem Kehrwert des Brechungsindex. Beispiel Wasser: Gemäß obiger Tabelle hat Wasser eine Brechzahl von 1,333; dadurch ergibt sich als Grenzwinkel αG=48,6°. Tritt also ein Lichtstrahl unter Wasser mit einem Winkel von 50° gegen die Oberfläche, so findet bereits eine Totalreflexion statt, d.h. der Lichtstrahl taucht nicht mehr aus dem Wasser auf.
Anwendung der Totalreflexion im Lichtwellenleiter
Während der Effekt der Totalreflexion zunächst wie ein ungewünschter Störeffekt erscheinen mag, so gibt es dennoch eine fortschrittliche Anwendung dafür, nämlich in Lichtwellenleitern. Die folgende Abbildung zeigt einen solchen Lichtwellenleiter im Querschnitt. Er besteht aus einem Mantel und einem Kern. Hauptprinzip ist, dass der Leiterkern einen höheren Brechungsindex als der Leitermantel hat. Man nennt einen solchen Lichtwellenleiter auch Stufenindexfaser. Tritt nun ein Lichtstrahl von links in den Lichtwellenleiter ein, so wird dieser an der Grenzfläche zwischen Kern und Mantel immer wieder total reflektiert, bis er schließlich am anderen Ende des Kabels wieder austritt.
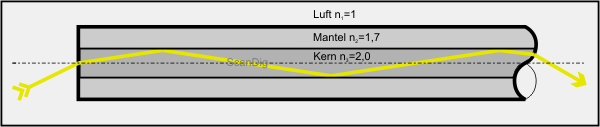
Im obigen Bild ist für den Mantel ein Brechungsindex von 1,7 und für den Kern von 2,0 eingetragen; die umgebende Luft hat einen Brechungsindex von 1. Die Leitung von Licht in einem Kabel funktioniert auch wenn der Lichtwellenleiter gekrümmt ist. Auf diese Weise kann ein Lichtstrahl quasi um mehrere Ecken gelenkt werden. Die oben dargestellte Stufenindexfaser besteht aus zwei Materialien mit jeweils unterschiedlichem Brechungsindex. In sogenannten Gradientenfasern steigt der Brechungsindex vom Mantel bis zum innersten Kern kontinuierlich an, so dass sich im Leiterinneren kontinuierliche Bögen des Lichtstrahles ergeben.
Verschiebung eines Lichtstrahls mit Hilfe einer planparallelen Glasplatte
Betrachten wir als weiteres Beispiel den Durchgang eines Lichtstrahls durch eine planparallele Platte. In der folgenden Abbildung ist dargestellt, wie ein Lichtstrahl von oben rechts durch eine solche Glasplatte durchtritt.
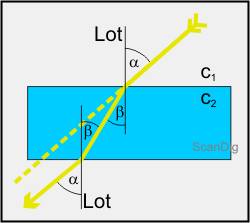
Der Lichtstrahl tritt mit einem Winkel α auf die Glasplatte und wird gebrochen. Da die Glasplatte ein optisch dichteres Medium als die umgebende Luft ist, wird der Lichtstrahl zum Einfallslot hin gebrochen. Der Winkel β ist also kleiner als der Eintrittswinkel α. Der Lichtstrahl durchquert dann geradlinig die Glasplatte bis er erneut an die untere Grenzfläche trifft.
Auf die untere Grenzfläche trifft der Lichtstrahl mit dem Winkel β. Beim Austritt aus der Glasplatte gilt der umgekehrte Fall wie beim obigen Eintritt: Der Lichtstrahl wird vom Lot weggebrochen. Es ist anschaulich und mit der Gleichung 2 leicht ableitbar, dass der Austrittswinkel α gleich dem ursprünglichen Eintrittswinkel α in die Glasplatte ist. Der Lichtstrahl tritt also unter demselben Winkel wieder aus wie er eingetreten ist. Das bedeutet, dass der Lichtstrahl seine Richtung beim Durchgang durch die planparallele Glasplatte nicht ändert. Jedoch erfolgt eine Parallelverschiebung des Lichtstrahls. Mit Hilfe einer Glasplatte kann man also einen Lichtstrahl einfach um ein paar Zentimenter verrücken. Anhand der Abbildung wird klar, dass die Parallelverschiebung umso größer ist je dicker die Glasplatte ist, d.h. desto mehr Weg der Lichtstrahl im Innern der Glasplatte zurücklegt ehe er wieder austritt.
Umlenkung eines Lichtstrahls mit Hilfe eines Prismas
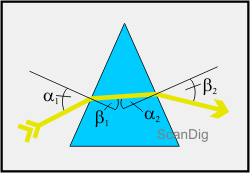
Gerade haben wir am Beispiel einer planparallelen Glasplatte gesehen, wie ein Lichtstrahl nur verschoben aber nicht umgelenkt wird. Um nun die Richtung eines Lichtstrahls zu ändern verwenden wir ein Glasprisma wie es in der folgenden Abbildung dargestellt ist. Der Lichtstrahl, der von links unten kommt, trifft auf die linke Seite des Glasprismas und wird dort gebrochen. Da das Glas im Vergleich zur umgebenden Luft das optisch dichtere Medium ist, wird der Lichtstrahl zum Einfallslot hingebrochen; der Winkel β1 ist also kleiner als der Einfallswinkel α1.
Im Innern des Glasprismas verläuft der Lichtstrahl geradlinig weiter bis er an die zweite Kante des Prismas trifft. Dort gilt wieder das Brechungsgesetz, wobei ein Übergang vom optisch dichteren ins optisch dünnere Medium stattfindet. Der Lichtstrahl, der also unter dem Eintrittswinkel α2 auf die Grenzfläche trifft, wird vom Lot weggebrochen und tritt mit dem Winkel β2 aus dem Prisma aus. Anhand der Abbildung wird ersichtlich, dass der Lichtstrahl am Prisma also zwei Mal in die gleiche Richtung abgelenkt wird. Insgesamt hat das Glasprisma also die Wirkung, dass der Lichtstrahl von seiner ursprünglichen Richtung abgelenkt wird.

An dieser Stelle möchte ich noch bemerken, dass der Brechungsindex keine Konstante ist, auch wenn er sich für jedes Medium wie oben gezeigt individuell berechnen und angeben lässt. Vielmehr ist die Brechzahl abhängig von der Wellenlänge des Lichts. Dass dem so ist, lässt sich beweisen, indem man einen Lichtstrahl mit weißem Sonnenlicht durch ein Glasprisma schickt und das austretende Farbspektrum mit einem Schirm auffängt. Auf dem Schirm erkennt man die sichtbaren Spektralfarben des weißen Lichts wieder und man erkennt die bekannten Regenbogenfarben. Licht mit kleiner Wellenlänge (blaues, ultraviolettes Licht) wird gemäß der Abbildung also stärker gebrochen als Licht mit großer Wellenlänge (rotes Licht).
Umlenkung von Lichtstrahlen mit einem Umkehrprisma
Im vorigen Kapitel haben wir gesehen, wie man mit Hilfe eines Prismas die Richtung eines Lichtstrahles leicht ändern kann; dabei haben wir ein gleichschenkliges, fast gleichseitiges Prisma verwendet. Ein Spezialfall von Prismen sind sogenannte Umlenk- oder Umkehrprismen, deren beiden Katheten im rechten Winkel zueinander stehen, so dass sich in der Seitenansicht die Figur eines rechtwinkligen Dreiecks ergibt.
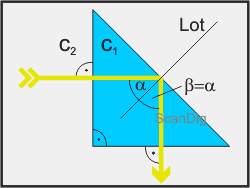
Die nebenstehende Abbildung zeigt ein solches Umkehrprisma im Querschnitt; die beiden kleineren Seiten des Prismas stehen im rechten Winkel zueinander. Schickt man von der linken Seite aus einen Lichtstrahl senkrecht auf die Prismenkante, so wird dieser nicht abgelenkt und bewegt sich im Innern des Prismas fort bis er auf die Hypotenuse trifft. Da es sich um ein rechtwinkliges Prisma handelt trifft der Lichtstrahl unter einem Winkel von α = 45° auf die lange Seite des Prismas. Ein Umkehrprisma zeichnet sich durch eine derartige Materialbeschaffenheit aus, dass bereits bei einem Winkel von 45° der Grenzwinkel erreicht ist, also Totalreflexion eintritt. Demzufolge tritt der Lichtstrahl an der Hypotenuse nicht aus dem Prisma aus sondern wird im gleichen Winkel zum Lot reflektiert. Der Ausfallswinkel β ist also gleich dem Einfallswinkel β = α = 45°. Auf die zweite Seitenkante des Umkehrprismas trifft der reflektierte Lichtstrahl wiederum mit einem Winkel von 90°, so dass er nicht abgelenkt wird. Insgesamt bewirkt dieses Umkehrprisma also eine Ablenkung des einfallenden Lichstrahles um exakt 90°.
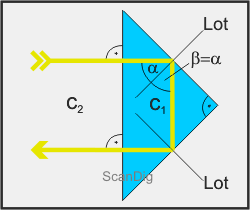
In der nebenstehenden Abbildung wird dasselbe Umkehrprisma wie im vorigen Beispiel verwendet, also wieder mit einem rechtwinkligen Dreieck als Querschnitt. Dieses Mal leiten wir den Lichtstrahl jedoch nicht senkrecht auf eine Kathete sondern auf die Hypotenuse ein. Tritt der von links einfallende Lichtstrahl senkrecht auf die lange Seite des Umkehrprismas so wird dieser nicht abgelenkt und bewegt sich im Inneren des Prismas weiter bis er auf die obere Kathete des Dreiecks gelangt. Dort trifft er in einem Winkel von α = 45° auf und wird im Winkel β = α = 45° total reflektiert, da die Materialbeschaffenheit des Umkehrprismas bereits bei 45° den Grenzwinkel garantiert. Der reflektierte Lichtstrahl bewegt sich im Inneren des Prismas senkrecht nach unten bis er auf die zweite Kathete trifft, wiederum mit einem Einfallswinkel von α = 45°. Wiederum findet eine Totalreflexion des Lichstrahles statt, so dass dieser im Prisma-Inneren nach links abgelenkt wird bis er erneut auf die Hypotenuse trifft. Da der Lichtstrahl durch die zweimalige Ablenkung um jeweils 45° senkrecht auf die Hypotenuse trifft verlässt er das Umkehrprisma ohne weitere Ablenkung. Insgesamt wird der Lichtstrahl durch die zweimalige Reflexion also um 180° abgelenkt; die Richtung des einfallenden Lichstrahles wird durch ein solches Umkehrprisma also umgedreht und parallel verschoben. Man spricht bei einer solchen doppelten Umlenkung auch von einem doppelreflektierenden Prisma.
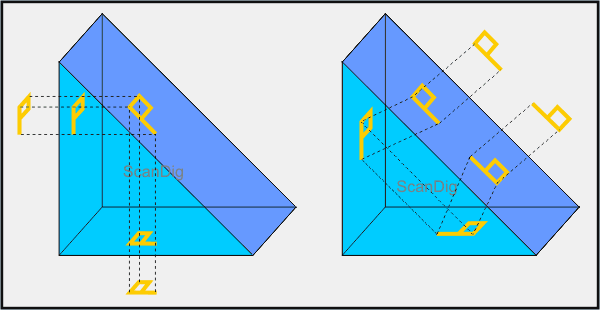
Betrachten wir noch die beiden Beispiele im dreidimensionalen Raum. Die nachfolgende Abbildung zeigt in der linken Bildhälfte, wie ein Strahlenbündel (ein Bild) von links in das Prisma eintaucht und dieses an der unteren Seite wieder verlässt. Man erkennt, dass das Bild lediglich um 90° gedreht wird. Bei der doppelten Umlenkung hingegen in der rechten Bildhälfte wird das Bild durch die zweifache Reflexion auf den Kopf gestellt. Das Bild wird also nicht nur umgelenkt und parallel verschoben sondern auch gespiegelt. Daher auch der Fachbegriff Umkehrprisma. Halten wir dies fest:
Ein Umkehrprisma lenkt eintreffende Lichtstrahlen um 180° um. Dabei entsteht ein umgekehrtes, auf dem Kopf stehendes Bild.
Schaltet man zwei solcher Umkehrprismen hintereinander, wobei das zweite gegenüber dem ersten um 90° gedreht ist, dann wird das Bild nicht nur horizontal sondern auch vertikal gespiegelt. Eine solche Anordnung zweier Umkehrprismen wird nach dem Erfinder Ignazio Porro auch Porroprisma genannt und sorgt zum Beispiel in Feldstechern oder Fernrohren für ein seitenrichtiges und aufrechtes Bild.
In der Optik werden Umlenkprismen vielfach eingesetzt, zum Beispiel in Spiegelreflexkameras für den Sucher oder in Fernrohren. Durch mehrfache Hintereinander-Anordnung solcher Umkehrprismen lässt sich ein Lichtstrahl beliebig umlenken und verschieben bzw. lässt sich ein Bild beliebig spiegeln. Dies ermöglicht bei vielen optischen Geräten wie Kameras, Feldstechern oder Teleskopen kleinere, kompaktere Bauweisen.
Bleibt abschließend noch die Frage, welchen Vorteil Umkehrprismen gegenüber einfachen Spiegeln haben. Ein Umkehrprisma ist ein einfacher Glaskörper, der dank der rechtwinkligen Außernseiten leicht zu montieren und zu justieren ist; die Justierung eines Spiegels im 45° Winkel ist aufwändiger. Hinzu kommt, dass bei einem Umkehrprisma die Lichtumlenkung alleine durch die natürliche Materialbeschaffenheit zustande kommt; bei einem Spiegel muss die Oberfläche hochwertig versilbert werden, damit keine Streuverluste entstehen. Eine 180° Umlenkung könnte zwar durch einen einzigen Spiegel leichter erfolgen als durch den Einsatz eines Prismas, dann würde das reflektierte Licht aber genau auf das einfallende Licht treffen; bei einem Umkehrprisma findet außer der 180°-Reflexion auch eine Parallelverschiebung des einfallenden Lichtstrahles statt.
Zurück zum Inhaltsverzeichnis Grundlagen der Fotografie
|